xgboost의 논문은 생각보다 양이 많고 읽기가 쉽지는 않다.
https://www.kdd.org/kdd2016/papers/files/rfp0697-chenAemb.pdf
시작하기전에, XGBoost논문에서는 부스팅에 관한 친절한 설명이 먼저 되어있다. 따라서 이를 좀더 쫓아가서 XGBoost를 이해하기전에 GBDT에 대해 더 이해해본다.
GBDT 기본 이해
부스팅은 여러 트리를 합치는 방식(Additive)으로, 계속해서 발전해나가는 방식을 쓰고는 한다. 어떻게 발전시키는지에 대해서는 바로 다음과 같은 목적함수을 최소화하는데, 시그마로 보아하면 한두개의 예측기가 아니라 여러개의 예측기의 loss로 부터 구함을 알수있다.

위의 식에서, 유클리디안 공간을 이용하는 optimization은 쓸수 없으니, 부스팅에서 사용하는 방법에서와 같이 조금씩 어떠한 식을 더해나가면서 수정하는 모델을 만들어낼 수 있다.

그리고 테일러 전개를 통해 2차 다항식으로 근사한 후, 상수항을 빼버리면 다음과 같다. 자세한 방법론은 테일러 정리를 찾으면 된다.

그리고 고정된 트리 구조 q 에 대해서 정리하면 다음과 같다.

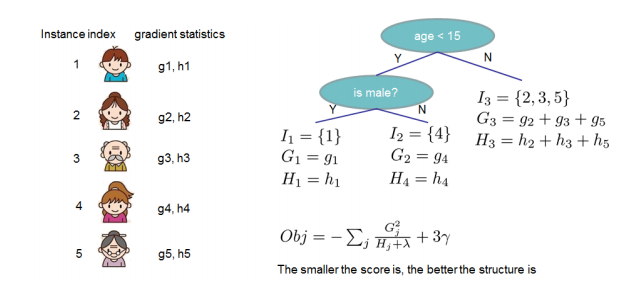
다만 생성가능한 모든 트리구조를 다 만들어 내는것은 불가능하므로, 하나씩 더해가는 구조로 이를 greedy방식으로 유추하자면 leaf가 하나인 트리부터 점수를 매기는데 이를 분기할때의 기준으로 삼을 수 있다. 따라서 최종적으로 분기 된 나무와 그전의 나무의 차이를 구해주면 정보이득으로 계산한다.

만약 정보이득이 정규화항보다 작다면 이 분기는 추가할 필요가 없다.
Shrinkage
eta, 혹은 learning rate이라고 부른 파라미터로, 부스팅은 한번에 모든 데이터를 학습하는게 아니라 점진적으로 하나씩 더해가면서 모델을 개선하게 만든다. 이 점진적으로 개선하는 데에 대한 파라미터이다. 당연히 learning rate을 통해 미세하게 성능을 앞서게 만들수 있다.
Column Subsampling
컬럼 부분 이용은 랜덤포레스트에서 이용되기도 하여 다양성을 높이고 오버피팅을 낮추는 역할을 한다. xgboost이후의 구현체들도 모두 지원하고 있다.
Exact Greedy Algorithm
성능은 제일 좋은 편이지만 node마다 계속 분기지점을 찾아야하기 때문에 시간이 오래걸린다.

Approximate Algorithm
분기를 하기 위해서는 먼저 정렬을 하고 여기에서 최적지점을 찾아야 하는데, 모든 데이터를 죄다 정렬해놓고 정확한 분기 지점을 찾기에는 계산시간이 굉장히 오래걸릴수 있다. 따라서 일종의 히스토그램을 이용하여 계산을 하게 되는데 데이터 전체를 대상으로 이를 구성하든지, 혹은 split할때마다 이를 구성할수있는데 전자는 시간이 짧은 반면 조금더 자세히 구간을 나눠야 하고 후자는 시간이 오래걸리지만 같은 조건이면 성능은 더 좋을 수 있다.

Weighted Quantile Sketch
XGBoost는 히스토그램을 이용한 방법에서 Weighted Quantile을 이용해서 분기지점을 찾는다. 이는 lightGBM에서는 히스토그램으로 표현되는데, 단순히 모든 데이터러를 훑는것이 아니라, 정렬되어있는 상태에서의 분위를 찾아 이들을 분기 후보로 놔둔다. 다 훑지 않기 떄문에 빠르다. 다만, Weighted인 이유는 다음에 supplement paper에 자세히 있는데, 링크가 죽어서 현재는 접속이 안되는중..
http://homes.cs.washington.edu/˜tqchen/pdf/xgboost-supp.pdf
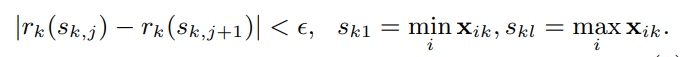
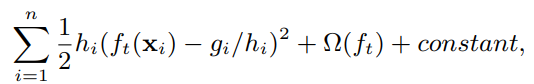
Sparsity-aware Split Finding
분기를 따라갈때 default값을 따라 가도록 하면, 값이 결측치더라도 기본값을 따라갈수 있게 하며, 이는 훈련과정중에 최적의 기본값을 산출하도록 훈련할 수 있다. xgboost에서는 결측치에 대해서 특별히 신경쓸 수 있기 때문에 훨씬 빠르다.

시스템적으로 속도를 향상시킬수 있는 방법은 다음을 언급한다.
- cache aware access
- out-of-core computation
XGBoost에서 제공하는 기능
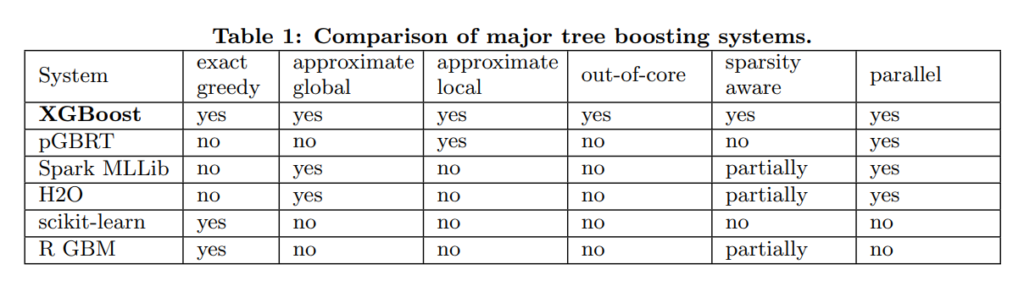
XGBoost에서는 위와같이 꽤나 많은 노력을 했음을 알수있다.